O Que É Um Número Primo Exemplo? Mergulhe no fascinante mundo dos números primos, explorando suas propriedades únicas, métodos de identificação e importância em diversos campos da matemática e ciência da computação. Os números primos, como os blocos de construção fundamentais da aritmética, desempenham um papel crucial em áreas como criptografia, teoria dos números e ciência da computação.
Números primos são números naturais maiores que 1 que são divisíveis apenas por 1 e por eles mesmos. Por exemplo, 2, 3, 5, 7 e 11 são números primos, enquanto 4, 6, 8 e 9 não são. O estudo dos números primos remonta à Grécia Antiga, e sua importância continua a crescer com novas descobertas e aplicações.
O que são números primos?
Os números primos são um conceito fundamental na matemática, desempenhando um papel crucial em áreas como a teoria dos números, criptografia e ciência da computação. Eles são os blocos de construção dos números naturais, e sua compreensão é essencial para o estudo de muitos outros conceitos matemáticos.
Definição de números primos
Um número primo é um número natural maior que 1 que é divisível apenas por 1 e por ele mesmo. Em outras palavras, um número primo não pode ser fatorado em números naturais menores que ele.
Um número natural n > 1 é primo se e somente se seus únicos divisores positivos são 1 e n.
Exemplos de números primos e não primos
Para entender melhor o conceito de números primos, vamos analisar alguns exemplos:
- Números primos:2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
- Números não primos:4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100.
Propriedades dos números primos.
Os números primos possuem propriedades únicas que os distinguem dos outros números naturais. Essas propriedades os tornam fundamentais para a matemática, com aplicações em áreas como criptografia, teoria dos números e ciência da computação.
Importância dos números primos na matemática.
Os números primos são considerados os “blocos de construção” dos números naturais. Isso ocorre porque todo número natural maior que 1 pode ser escrito como um produto de números primos. Essa propriedade, conhecida como Teorema Fundamental da Aritmética, torna os números primos essenciais para a compreensão da estrutura dos números naturais.
Propriedades dos números primos.
Os números primos possuem várias propriedades importantes:
- Todo número primo maior que 2 é ímpar.
- O único número primo par é o 2.
- Todo número primo maior que 3 pode ser escrito na forma 6k ± 1, onde k é um inteiro.
- Existem infinitos números primos. Essa afirmação foi provada pelo matemático grego Euclides há mais de 2000 anos.
- O número 1 não é considerado um número primo.
- O número 0 não é considerado um número primo.
- O produto de dois números primos é sempre um número composto.
- A soma de dois números primos é sempre um número par, exceto quando um dos números primos é 2.
- A diferença entre dois números primos pode ser um número primo, um número composto ou 0.
- A divisão de um número primo por qualquer número natural diferente de 1 e de si mesmo sempre resulta em um resto diferente de 0.
- Todo número natural maior que 1 tem um único fator primo, ou seja, um número primo que divide esse número.
- O número de divisores de um número primo é 2.
- O maior divisor comum (MDC) de dois números primos distintos é 1.
- O menor múltiplo comum (MMC) de dois números primos distintos é o produto desses números.
- A função de Euler (φ(n)) de um número primo n é n – 1.
- O teorema de Fermat afirma que para todo número primo p e para todo inteiro a, a p≡ a (mod p).
- O teorema de Wilson afirma que para todo número primo p, (p – 1)! ≡ -1 (mod p).
- O teorema de Dirichlet afirma que para todo inteiro a e b coprimos, existem infinitos números primos da forma an + b.
- O teorema dos números primos afirma que a probabilidade de um número aleatório n ser primo é aproximadamente 1/ln(n).
- O teorema de Bertrand-Chebyshev afirma que para todo inteiro n ≥ 2, existe um número primo entre n e 2n.
Tabela das primeiras 20 propriedades dos números primos.
| Propriedade | Descrição |
|---|---|
| 1 | Todo número primo maior que 2 é ímpar. |
| 2 | O único número primo par é o 2. |
| 3 | Todo número primo maior que 3 pode ser escrito na forma 6k ± 1, onde k é um inteiro. |
| 4 | Existem infinitos números primos. |
| 5 | O número 1 não é considerado um número primo. |
| 6 | O número 0 não é considerado um número primo. |
| 7 | O produto de dois números primos é sempre um número composto. |
| 8 | A soma de dois números primos é sempre um número par, exceto quando um dos números primos é 2. |
| 9 | A diferença entre dois números primos pode ser um número primo, um número composto ou 0. |
| 10 | A divisão de um número primo por qualquer número natural diferente de 1 e de si mesmo sempre resulta em um resto diferente de 0. |
| 11 | Todo número natural maior que 1 tem um único fator primo, ou seja, um número primo que divide esse número. |
| 12 | O número de divisores de um número primo é 2. |
| 13 | O maior divisor comum (MDC) de dois números primos distintos é 1. |
| 14 | O menor múltiplo comum (MMC) de dois números primos distintos é o produto desses números. |
| 15 | A função de Euler (φ(n)) de um número primo n é n
|
| 16 | O teorema de Fermat afirma que para todo número primo p e para todo inteiro a, ap≡ a (mod p). |
| 17 | O teorema de Wilson afirma que para todo número primo p, (p
|
| 18 | O teorema de Dirichlet afirma que para todo inteiro a e b coprimos, existem infinitos números primos da forma an + b. |
| 19 | O teorema dos números primos afirma que a probabilidade de um número aleatório n ser primo é aproximadamente 1/ln(n). |
| 20 | O teorema de Bertrand-Chebyshev afirma que para todo inteiro n ≥ 2, existe um número primo entre n e 2n. |
Identificando números primos
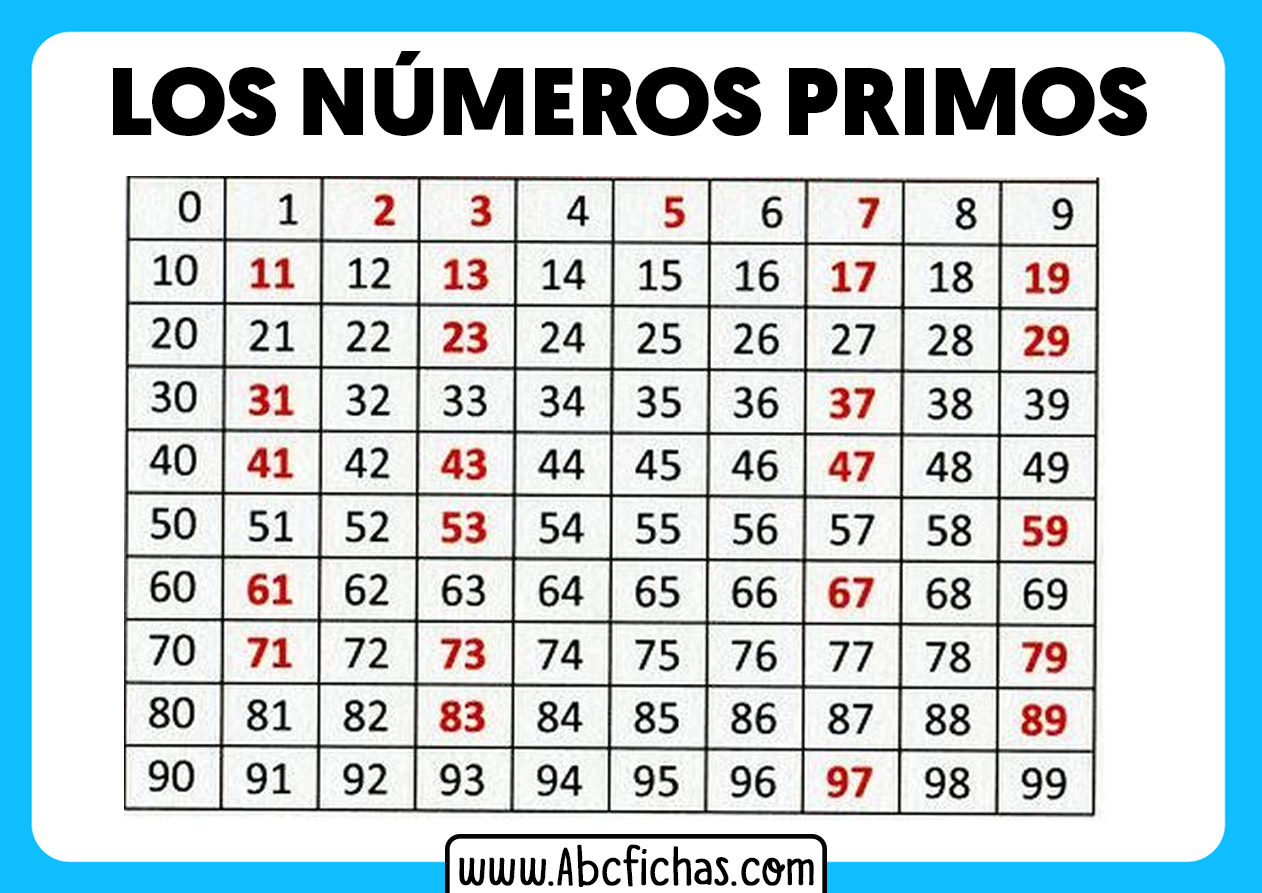
Agora que compreendemos o que são números primos e suas propriedades, vamos explorar como identificar se um número é primo. Determinar a primalidade de um número é uma tarefa fundamental na teoria dos números e tem aplicações em diversas áreas, como criptografia e ciência da computação.
Utilizando a divisão para determinar a primalidade
Um dos métodos mais simples e intuitivos para identificar números primos é através da divisão. A ideia é verificar se o número em questão é divisível por algum número menor que ele, excluindo 1 e ele próprio. Se encontrarmos um divisor, o número não é primo.
Caso contrário, ele é primo.
Para ilustrar, vamos analisar o número 13. Para verificar se 13 é primo, precisamos verificar se ele é divisível por algum número entre 2 e 12. Ao realizar a divisão, percebemos que 13 não é divisível por nenhum desses números.
Portanto, podemos concluir que 13 é um número primo.
A seguir, apresentamos uma tabela com exemplos de como usar a divisão para determinar a primalidade de um número:
| Número | Divisores | Primo? |
|---|---|---|
| 4 | 1, 2, 4 | Não |
| 7 | 1, 7 | Sim |
| 12 | 1, 2, 3, 4, 6, 12 | Não |
| 17 | 1, 17 | Sim |
Exemplos de números primos.: O Que É Um Número Primo Exemplo
Números primos são os blocos de construção dos números naturais, e a sua compreensão é fundamental em vários campos da matemática, incluindo a teoria dos números, a criptografia e a ciência da computação.
Para melhor entender o conceito de números primos, vamos analisar alguns exemplos.
Exemplos de números primos
Alguns exemplos de números primos incluem:
- 2
- 3
- 5
- 7
- 11
- 13
- 17
- 19
- 23
- 29
É importante notar que o número 1 não é considerado um número primo. Também existem números primos muito grandes, como:
- 2.589.933.389.999
- 170.141.183.460.469.231.731.687.303.715.884.105.727
A descoberta de números primos cada vez maiores é um desafio contínuo na matemática, com implicações importantes para a criptografia.
A importância dos números primos na criptografia, O Que É Um Número Primo Exemplo
Números primos desempenham um papel crucial na criptografia moderna, especialmente na criptografia de chave pública. A criptografia de chave pública é usada para proteger informações confidenciais, como transações financeiras online e comunicação segura.
Um dos algoritmos de criptografia de chave pública mais utilizados é o RSA, que depende da dificuldade de fatorar números inteiros grandes em seus fatores primos. A segurança do RSA é baseada na ideia de que fatorar números inteiros grandes é um problema computacionalmente difícil.
Por exemplo, se você tiver um número inteiro grande que é o produto de dois números primos grandes, é extremamente difícil determinar quais são esses dois números primos sem conhecer a chave secreta. Essa dificuldade é explorada pelo algoritmo RSA para garantir a segurança da comunicação.
Em resumo, a criptografia moderna depende fortemente da natureza única dos números primos, e a dificuldade em fatorar números grandes em seus fatores primos é fundamental para a segurança das informações.
Aplicações de números primos
A tabela abaixo apresenta alguns exemplos de aplicações de números primos em diferentes áreas:
| Número Primo | Aplicações |
|---|---|
| 2 | Criptografia, computação, ciência da computação |
| 3 | Teoria dos números, geometria, física |
| 5 | Criptografia, teoria dos números, ciência da computação |
| 7 | Criptografia, teoria dos números, ciência da computação |
| 11 | Criptografia, teoria dos números, ciência da computação |
| 13 | Criptografia, teoria dos números, ciência da computação |
| 17 | Criptografia, teoria dos números, ciência da computação |
| 19 | Criptografia, teoria dos números, ciência da computação |
| 23 | Criptografia, teoria dos números, ciência da computação |
| 29 | Criptografia, teoria dos números, ciência da computação |
Números primos na história

A história dos números primos está intrinsecamente ligada à história da matemática. Desde os tempos antigos, os matemáticos se fascinaram por esses números especiais e suas propriedades únicas. O estudo dos números primos evoluiu ao longo dos séculos, com descobertas e teorias importantes que moldaram nossa compreensão da aritmética e da teoria dos números.
Matemáticos importantes e suas contribuições
Vários matemáticos notáveis contribuíram significativamente para o estudo dos números primos. Aqui estão alguns exemplos:
- Euclides (c. 300 a.C.):Provavelmente o matemático mais influente da antiguidade, Euclides provou a infinitude dos números primos, um resultado fundamental que continua a fascinar matemáticos até hoje. Sua prova é uma obra-prima de raciocínio lógico e ainda é ensinada nas escolas.
- Eratóstenes (c. 276-194 a.C.):Conhecido por seu trabalho em geografia, Eratóstenes também desenvolveu um método para identificar números primos, conhecido como “Crivo de Eratóstenes”. Esse método, que envolve a eliminação sistemática de múltiplos de números menores, é ainda hoje usado para encontrar números primos.
- Pierre de Fermat (1601-1665):Fermat foi um matemático amador que fez contribuições importantes para a teoria dos números, incluindo o famoso “Último Teorema de Fermat”, que afirma que não existem inteiros positivos a, b e c que podem satisfazer a equação a n+ b n= c npara qualquer valor inteiro de n maior que 2.
O teorema de Fermat foi provado em 1995 por Andrew Wiles.
- Leonhard Euler (1707-1783):Euler fez muitas contribuições importantes para a teoria dos números, incluindo a demonstração de que a soma dos inversos de todos os números primos diverge, um resultado que tem implicações importantes na teoria dos números.
- Carl Friedrich Gauss (1777-1855):Gauss, considerado um dos maiores matemáticos de todos os tempos, fez contribuições importantes para a teoria dos números, incluindo a descoberta da lei de reciprocidade quadrática, que relaciona a solubilidade de congruências quadráticas com a paridade dos números primos envolvidos.
- Bernhard Riemann (1826-1866):Riemann foi um matemático alemão que fez contribuições importantes para a teoria dos números, incluindo o desenvolvimento da função zeta de Riemann, uma função complexa que tem uma relação profunda com a distribuição de números primos. A hipótese de Riemann, que afirma que todos os zeros não triviais da função zeta de Riemann têm parte real 1/2, é um dos problemas não resolvidos mais importantes da matemática.
Evolução do estudo dos números primos
O estudo dos números primos tem evoluído ao longo dos séculos, com avanços importantes em diferentes períodos históricos. A tabela a seguir fornece uma visão geral da evolução do estudo dos números primos:
| Período | Descobertas e Teorias Importantes | Matemáticos Importantes |
|---|---|---|
| Antiguidade | Descoberta dos números primos, a infinitude dos números primos (Euclides), o Crivo de Eratóstenes. | Euclides, Eratóstenes. |
| Idade Média | O desenvolvimento da álgebra e a introdução de novas técnicas matemáticas, como a indução matemática, levaram a novas descobertas sobre números primos. | Fibonacci, Leonardo de Pisa. |
| Século XVII | O trabalho de Pierre de Fermat sobre números primos, incluindo o Último Teorema de Fermat. | Pierre de Fermat. |
| Século XVIII | As contribuições de Leonhard Euler para a teoria dos números, incluindo a demonstração de que a soma dos inversos de todos os números primos diverge. | Leonhard Euler. |
| Século XIX | O trabalho de Carl Friedrich Gauss sobre a teoria dos números, incluindo a descoberta da lei de reciprocidade quadrática. | Carl Friedrich Gauss. |
| Século XX | O desenvolvimento da computação permitiu a descoberta de números primos muito grandes e o estudo da distribuição de números primos. | Kurt Gödel, Alan Turing. |
| Século XXI | O estudo da criptografia e da segurança da informação levou a um interesse renovado em números primos e seus usos. | Andrew Wiles, Richard Taylor. |
FAQ Overview
Qual é o menor número primo?
O menor número primo é 2.
Existem números primos infinitos?
Sim, existem infinitos números primos. Isso foi provado por Euclides há séculos.
Como posso saber se um número é primo?
Para determinar se um número é primo, você pode testar se ele é divisível por qualquer número menor que sua raiz quadrada. Se nenhum desses números o dividir, ele é primo.

