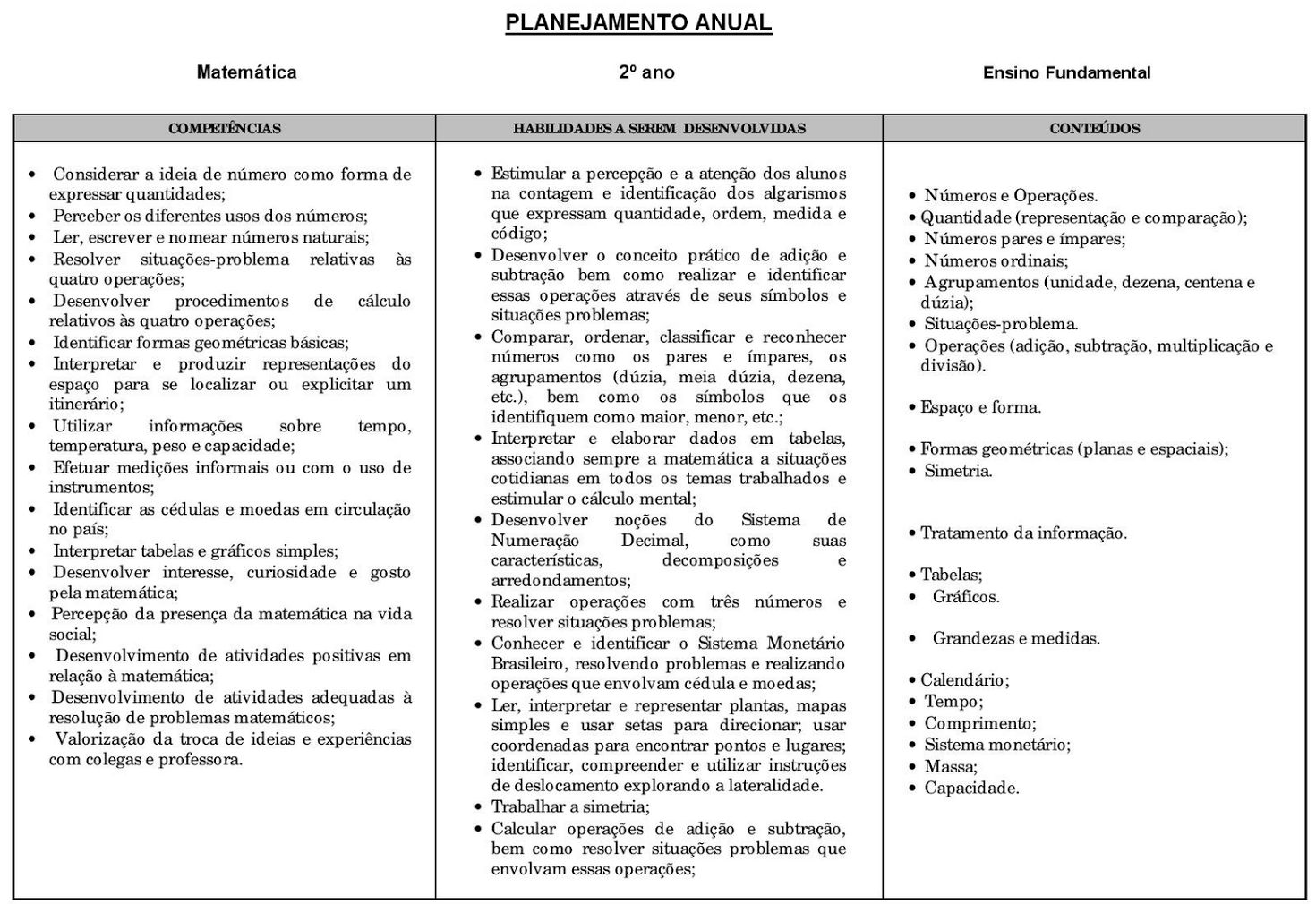
Exemplo De Plano De Aula De Matematica Ensino Fundamental Ii – Exemplo De Plano De Aula De Matemática Ensino Fundamental II apresenta uma abordagem sistemática para o planejamento de aulas eficazes de matemática no Ensino Fundamental II. Este documento explora a construção de planos de aula que consideram a contextualização dos conteúdos, a diversidade de metodologias de ensino e a utilização de recursos didáticos adequados para atender às necessidades dos alunos.
A ênfase está na criação de planos que promovam a aprendizagem significativa e o desenvolvimento de habilidades matemáticas essenciais para essa faixa etária.
Serão abordados temas como frações, geometria plana e porcentagem, com exemplos práticos de planos de aula que incluem objetivos de aprendizagem específicos, atividades diversificadas e estratégias de avaliação formativa. A discussão engloba a importância da integração de diferentes áreas do conhecimento, a adaptação do plano de aula às necessidades individuais dos alunos e a utilização de tecnologias digitais para enriquecer o processo de ensino-aprendizagem.
Planos de Aula de Matemática para o Ensino Fundamental II: Exemplo De Plano De Aula De Matematica Ensino Fundamental Ii
Um plano de aula eficaz para matemática no Ensino Fundamental II guia o processo de ensino-aprendizagem, assegurando que os alunos compreendam os conceitos matemáticos de forma significativa e desenvolvam habilidades essenciais para a resolução de problemas. A contextualização dos conteúdos é crucial para tornar a matemática relevante e interessante para os alunos dessa faixa etária, conectando-a com suas experiências cotidianas.
Elementos Essenciais de um Plano de Aula Eficaz
Um plano de aula eficaz para matemática no Ensino Fundamental II deve incluir: objetivos de aprendizagem claros e mensuráveis, conteúdos a serem abordados, metodologias de ensino adequadas, atividades diversificadas (exercícios, jogos, projetos), recursos didáticos apropriados, estratégias de avaliação e critérios de desempenho. A flexibilidade também é importante, permitindo adaptações de acordo com as necessidades individuais dos alunos.
Importância da Contextualização
Contextualizar os conteúdos matemáticos significa conectar os conceitos abstratos com situações reais da vida dos alunos. Por exemplo, ao ensinar frações, podemos usar exemplos de receitas culinárias, divisão de tarefas em grupo ou representações gráficas de dados coletados em pesquisas. Isso torna a aprendizagem mais significativa e engajadora, facilitando a compreensão e a retenção do conhecimento.
Tipos de Atividades em um Plano de Aula
As atividades devem ser diversificadas para atender aos diferentes estilos de aprendizagem. Exercícios tradicionais são importantes para a prática e consolidação dos conceitos, mas devem ser complementados por jogos, que promovem o aprendizado lúdico e a cooperação, e projetos, que permitem a aplicação dos conhecimentos em situações mais complexas e desafiadoras. A combinação dessas abordagens garante um aprendizado mais completo e significativo.
Exemplos de Planos de Aula
Apresentaremos exemplos de planos de aula para diferentes temas matemáticos, incluindo objetivos de aprendizagem específicos e mensuráveis, metodologias de ensino e recursos didáticos. Cada plano exemplifica uma abordagem prática e contextualizada.
Plano de Aula: Frações
Objetivos: Os alunos serão capazes de representar frações, comparar frações e resolver problemas envolvendo frações. Conteúdo: Conceito de fração, representação gráfica de frações, comparação de frações, operações com frações (adição e subtração). Metodologia: Uso de material concreto (barras de frações, pizzas), jogos de tabuleiro, resolução de problemas contextualizados. Recursos: Barras de frações, jogos, livro didático, quadro branco. Avaliação: Observação da participação em atividades, resolução de exercícios e avaliação escrita.
Plano de Aula: Geometria Plana
Objetivos: Os alunos serão capazes de identificar e classificar figuras geométricas planas, calcular perímetros e áreas de figuras planas. Conteúdo: Figuras geométricas planas (quadrado, retângulo, triângulo, círculo), perímetro, área. Metodologia: Uso de materiais concretos (geoplanos, sólidos geométricos), construção de figuras geométricas, resolução de problemas. Recursos: Geoplanos, sólidos geométricos, régua, compasso, livro didático. Avaliação: Observação da participação em atividades, construção de figuras geométricas e resolução de problemas.
Plano de Aula: Porcentagem, Exemplo De Plano De Aula De Matematica Ensino Fundamental Ii
Objetivos: Os alunos serão capazes de calcular porcentagens, resolver problemas envolvendo porcentagens e aplicar porcentagens em situações cotidianas. Conteúdo: Conceito de porcentagem, cálculo de porcentagem, aplicação de porcentagem em situações cotidianas (descontos, juros, impostos). Metodologia: Resolução de problemas contextualizados, uso de calculadora, jogos, trabalho em grupo. Recursos: Calculadora, livro didático, materiais de apoio (folhetos de propaganda com descontos). Avaliação: Resolução de problemas, avaliação escrita e apresentação de trabalhos em grupo.
Plano de Aula: Integração Matemática e Ciências
Objetivos: Os alunos serão capazes de aplicar conceitos matemáticos para resolver problemas relacionados a fenômenos científicos. Conteúdo: Medidas de temperatura, construção de gráficos, interpretação de dados. Metodologia: Experimentos científicos, coleta de dados, construção de gráficos, análise de resultados. Recursos: Termômetro, materiais para experimentos, papel milimetrado, softwares de planilhas. Avaliação: Relatório da experiência, análise dos dados e interpretação dos resultados.
Metodologias de Ensino
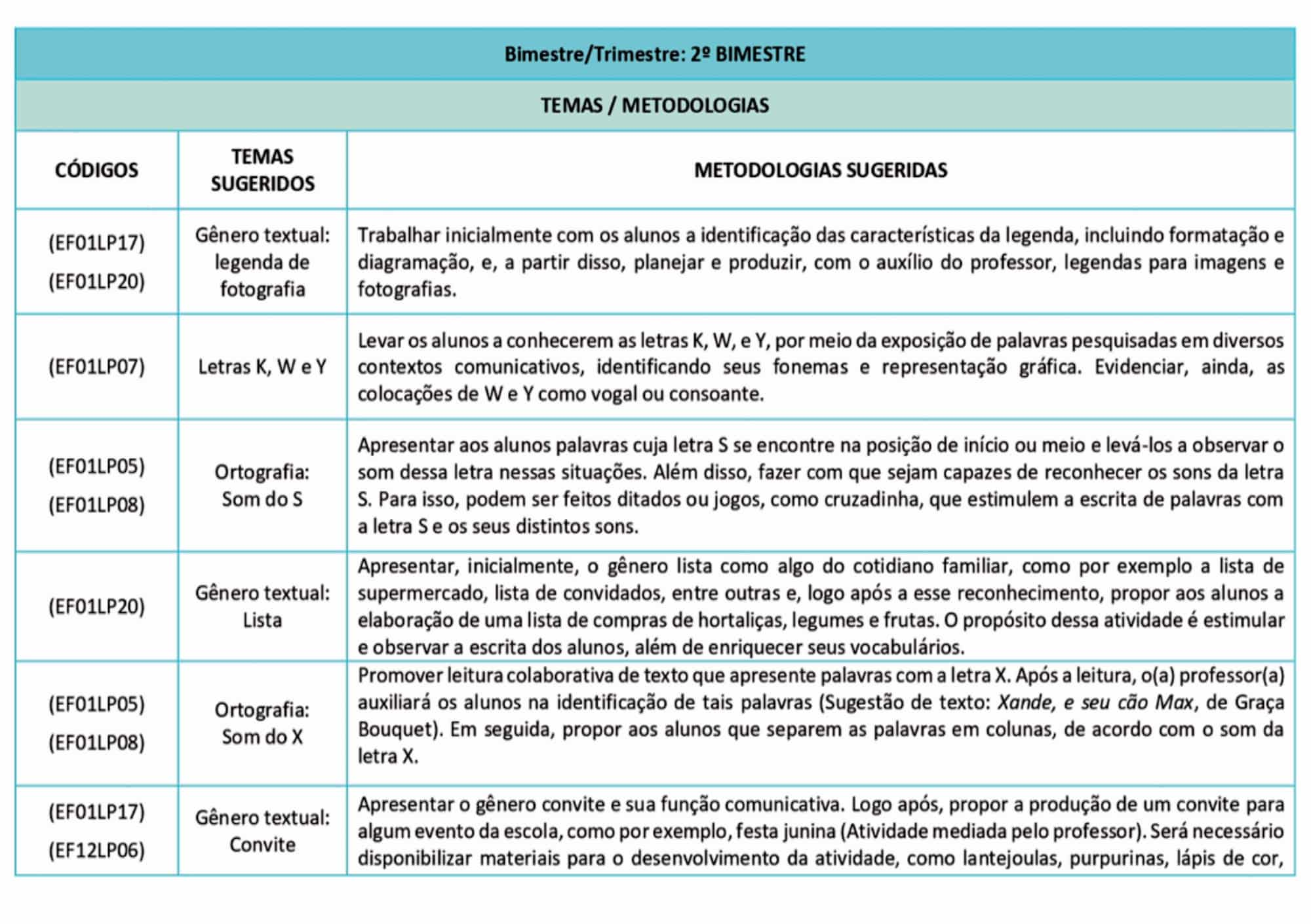
Diversas metodologias podem ser empregadas no ensino de matemática, cada uma com suas características e vantagens. A escolha da metodologia ideal dependerá dos objetivos de aprendizagem, dos recursos disponíveis e das características dos alunos.
Comparação de Metodologias
A metodologia construtivista enfatiza a construção do conhecimento pelo próprio aluno, enquanto a montessoriana promove a aprendizagem através da manipulação de materiais concretos e atividades autodirigidas. Ambas valorizam a experimentação e a descoberta, adaptando-se às necessidades individuais. Outras abordagens, como a resolução de problemas e o ensino por investigação, também são eficazes.
Utilização de Jogos e Atividades Lúdicas
Jogos e atividades lúdicas tornam o aprendizado de matemática mais divertido e engajador, estimulando a participação ativa dos alunos e promovendo a cooperação e a resolução de problemas em grupo. Eles podem ser adaptados para diferentes conteúdos matemáticos e níveis de dificuldade.
Importância da Avaliação Formativa
A avaliação formativa é um processo contínuo que acompanha o aprendizado dos alunos, fornecendo feedback constante e permitindo ajustes no processo de ensino. Ela deve ser integrada ao plano de aula, utilizando diferentes instrumentos como observação, questionários e atividades de autoavaliação.
Adaptação do Plano de Aula para Diferentes Estilos de Aprendizagem
É essencial adaptar o plano de aula para atender às necessidades de alunos com diferentes estilos de aprendizagem. Isso pode envolver a diversificação das atividades, o uso de diferentes recursos didáticos e a adoção de estratégias de ensino que considerem as preferências individuais dos alunos.
Recursos Didáticos
A escolha adequada dos recursos didáticos é fundamental para o sucesso do processo de ensino-aprendizagem. Materiais concretos, softwares educativos e tecnologias digitais podem enriquecer as aulas e tornar a aprendizagem mais significativa.
Recursos Didáticos e suas Aplicações
| Recurso Didático | Descrição | Tema Matemático | Exemplo de Atividade |
|---|---|---|---|
| Material Concreto (blocos lógicos) | Objetos manipuláveis que permitem a exploração de conceitos matemáticos. | Classificação, seriação, contagem | Construção de sequências, classificação por cor e forma. |
| Software Educativo (GeoGebra) | Programa de geometria dinâmica que permite a construção e manipulação de figuras geométricas. | Geometria Plana, Geometria Espacial | Construção de polígonos, exploração de propriedades geométricas. |
| Jogos de Tabuleiro | Jogos que envolvem conceitos matemáticos, como adição, subtração, multiplicação e divisão. | Operações básicas, probabilidade | Jogo da memória com operações matemáticas, jogo de tabuleiro com desafios de contagem. |
| Calculadora | Ferramenta que auxilia nos cálculos matemáticos, especialmente em operações mais complexas. | Operações com números decimais, porcentagens | Resolução de problemas que envolvem cálculos complexos. |
Utilização de Tecnologias Digitais
Computadores, tablets e outros dispositivos tecnológicos podem ser usados para enriquecer as aulas de matemática, oferecendo acesso a simulações, jogos educativos e recursos interativos. Plataformas online também oferecem atividades e exercícios que complementam o aprendizado em sala de aula.
Criando um Mapa Conceitual
Um mapa conceitual pode representar os conceitos matemáticos abordados em um plano de aula, mostrando as relações entre eles de forma visual e organizada. Ele pode ser criado manualmente ou utilizando softwares específicos. Por exemplo, para um plano de aula sobre frações, o mapa conceitual poderia mostrar os conceitos de numerador, denominador, frações equivalentes e operações com frações, com setas conectando os conceitos e mostrando suas relações.
Avaliação
A avaliação da aprendizagem em matemática deve ser abrangente e considerar diferentes instrumentos e critérios. A combinação de diferentes métodos garante uma avaliação mais justa e completa do desempenho dos alunos.
Instrumentos de Avaliação
Provas escritas, trabalhos individuais e em grupo, projetos, observação da participação em aula e autoavaliação são alguns dos instrumentos que podem ser utilizados para avaliar a aprendizagem dos alunos em matemática. A escolha dos instrumentos dependerá dos objetivos de aprendizagem e do conteúdo abordado.
Critérios de Avaliação
Os critérios de avaliação devem ser claros e específicos, definindo o que se espera que os alunos demonstrem em termos de conhecimento, habilidades e atitudes. Eles devem ser comunicados aos alunos desde o início do processo de ensino-aprendizagem.
Exemplo de Rubrica de Avaliação
Uma rubrica de avaliação para um projeto de matemática pode incluir critérios como clareza da apresentação, correção dos cálculos, criatividade e trabalho em equipe. Cada critério pode ter diferentes níveis de desempenho, com pontuações correspondentes.
Importância da Autoavaliação e Avaliação entre Pares
A autoavaliação e a avaliação entre pares promovem a metacognição e a reflexão sobre o próprio processo de aprendizagem. Elas ajudam os alunos a identificar seus pontos fortes e fracos, a definir metas de aprendizagem e a colaborar com os colegas.

