10 Exemplos De Quadrado Da Soma – Brainly: Aprenda a dominar o quadrado da soma com exemplos práticos e didáticos! Este guia descomplica essa fórmula matemática fundamental, mostrando como aplicá-la em diversos problemas, desde expressões algébricas simples até cálculos de áreas geométricas. Prepare-se para entender a fundo a fórmula (a+b)² = a² + 2ab + b² e suas infinitas aplicações.
Vamos explorar a fórmula do quadrado da soma, (a+b)², e como ela simplifica cálculos e resolve problemas aparentemente complexos. Veremos a diferença entre o quadrado da soma e o quadrado da diferença, e como identificar qual fórmula usar em cada situação. Através de exemplos passo a passo, você vai dominar a técnica e conseguir resolver problemas de forma eficiente e precisa.
Prepare-se para descobrir a beleza e a praticidade da matemática!
Aplicações e Exemplos do Quadrado da Soma
A fórmula do quadrado da soma, (a + b)² = a² + 2ab + b², é uma ferramenta fundamental na álgebra, com aplicações que vão além da simplificação de expressões. Sua compreensão permite resolver problemas em diversas áreas, desde a geometria até o cálculo de áreas e volumes. A seguir, exploraremos exemplos práticos que demonstram a utilidade dessa fórmula.
Dez Exemplos Distintos de Problemas Utilizando a Fórmula do Quadrado da Soma
A fórmula do quadrado da soma se mostra extremamente útil na resolução de diversos problemas. Sua aplicação simplifica cálculos e permite encontrar soluções de forma eficiente. Vejamos dez exemplos distintos:
- Calcular a área de um quadrado: Se o lado de um quadrado mede (x + 3) unidades, sua área é (x + 3)² = x² + 6x + 9 unidades quadradas.
- Simplificar expressões algébricas: A expressão (2x + 5)² pode ser simplificada para 4x² + 20x + 25 usando a fórmula.
- Resolver equações quadráticas: A equação (x + 2)² = 9 pode ser resolvida expandindo o quadrado da soma: x² + 4x + 4 = 9, resultando em x² + 4x – 5 = 0. Resolvendo essa equação, encontramos x = 1 ou x = -5.
- Calcular o volume de um cubo: Se a aresta de um cubo mede (y + 1) unidades, seu volume é (y + 1)³ = (y + 1)(y² + 2y + 1) = y³ + 3y² + 3y + 1 unidades cúbicas.
- Determinar a área de um retângulo: Um retângulo tem lados medindo (a + b) e (a + b). Sua área é (a + b)² = a² + 2ab + b².
- Simplificar expressões com raízes quadradas: √( (x+4)² ) = x+4, considerando x ≥ -4.
- Resolver problemas de física: Em um problema de cinemática, a distância percorrida por um objeto pode ser representada por uma expressão que envolve o quadrado da soma.
- Resolver problemas de geometria analítica: A distância entre dois pontos pode ser calculada usando a fórmula da distância, que pode ser simplificada com o quadrado da soma em certos casos.
- Encontrar o desenvolvimento de um binômio ao quadrado: (3a + 2b)² = 9a² + 12ab + 4b²
- Simplificar expressões em problemas de probabilidade: Em alguns problemas de probabilidade, expressões que envolvem o quadrado da soma podem ser simplificadas para facilitar os cálculos.
Comparação de Métodos para Resolver um Problema Usando o Quadrado da Soma
Vamos considerar o problema de calcular (2x + 3)²: Método 1: Aplicação direta da fórmulaUtilizando a fórmula (a + b)² = a² + 2ab + b², temos a = 2x e b = 3. Substituindo, obtemos (2x)² + 2(2x)(3) + (3)² = 4x² + 12x + 9. Método 2: Multiplicação diretaPodemos expandir o quadrado multiplicando (2x + 3) por si mesmo: (2x + 3)(2x + 3) = 2x(2x) + 2x(3) + 3(2x) + 3(3) = 4x² + 6x + 6x + 9 = 4x² + 12x + 9.Ambos os métodos levam ao mesmo resultado, 4x² + 12x + 9.
O primeiro método, utilizando a fórmula, é mais eficiente e requer menos etapas.
Problema Original e Solução Utilizando a Fórmula do Quadrado da Soma
Um jardim retangular tem comprimento (x + 5) metros e largura (x + 2) metros. Qual é a área do jardim?Solução: A área de um retângulo é dada pelo produto do comprimento pela largura. Portanto, a área do jardim é (x + 5)(x + 2). Podemos usar a fórmula do quadrado da soma se reescrevermos a expressão como (x + 3.5 + 1.5)(x + 3.5 – 1.5) e aplicar a diferença de quadrados, ou então, desenvolver a multiplicação diretamente: (x + 5)(x + 2) = x² + 2x + 5x + 10 = x² + 7x + 10 metros quadrados.
Simplificação de Expressões Algébricas Complexas Usando o Quadrado da Soma, 10 Exemplos De Quadrado Da Soma – Brainly
A fórmula do quadrado da soma pode ser usada para simplificar expressões algébricas complexas, como a seguinte: (x² + 4x + 4) + (2x + 4)(x – 1) + (x – 1)². Observando que x² + 4x + 4 = (x + 2)² e que (x – 1)² representa o quadrado de uma diferença, podemos simplificar a expressão.
Ao desenvolver a expressão e agrupar os termos semelhantes, podemos verificar a simplificação.
Extensões e Aplicações Avançadas: 10 Exemplos De Quadrado Da Soma – Brainly
A fórmula do quadrado da soma, (a + b)² = a² + 2ab + b², é mais do que uma simples identidade algébrica; ela representa uma ferramenta poderosa com aplicações que se estendem além do cálculo algébrico básico. Sua compreensão aprofundada revela conexões importantes com a fatoração, a geometria e o cálculo de áreas, abrindo portas para a resolução de problemas mais complexos.A relação entre o quadrado da soma e a fatoração é intrínseca.
A fórmula nos permite fatorar expressões da forma a² + 2ab + b², transformando-as na forma mais compacta (a + b)². Essa capacidade de fatoração simplifica cálculos e permite a manipulação de expressões algébricas de forma mais eficiente. Por exemplo, ao fatorar x² + 6x + 9, reconhecemos que se trata de um quadrado da soma, onde a = x e b = 3, resultando em (x + 3)².
Essa fatoração é crucial na resolução de equações quadráticas e na simplificação de expressões racionais.
Relação com a Fatoração de Expressões Algébricas
A fórmula do quadrado da soma é fundamental para a fatoração de trinômios quadrados perfeitos. Reconhecer a estrutura a² + 2ab + b² em uma expressão permite sua imediata fatoração para (a + b)². Isso simplifica cálculos e permite a resolução de equações e simplificação de expressões mais complexas. A habilidade de identificar e aplicar esse padrão de fatoração é essencial em diversos contextos matemáticos.
A recíproca também é verdadeira: a expansão de (a+b)² resulta em a² + 2ab + b², demonstrando a relação bidirecional entre a fórmula e o processo de fatoração.
Aplicações Geométricas da Fórmula do Quadrado da Soma
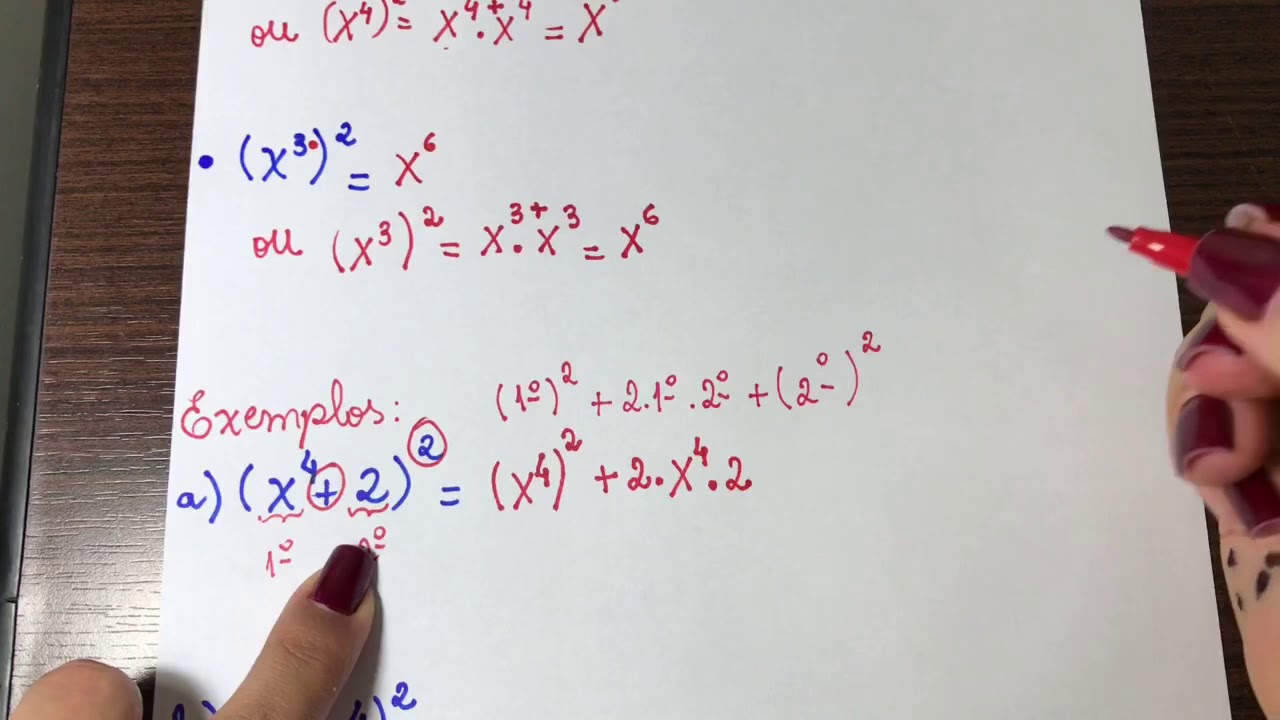
A fórmula do quadrado da soma possui uma interpretação geométrica clara e intuitiva, especialmente quando aplicada ao cálculo de áreas. Consideremos um quadrado com lado (a + b). Sua área é (a + b)². Dividindo esse quadrado em quatro regiões distintas, visualizamos a aplicação da fórmula: um quadrado de lado ‘a’ (área a²), um quadrado de lado ‘b’ (área b²), e dois retângulos com lados ‘a’ e ‘b’ (área 2ab cada).
A soma das áreas dessas quatro regiões (a² + 2ab + b²) corresponde à área total do quadrado maior, (a + b)².
Cálculo de Áreas de Figuras Geométricas

A fórmula (a + b)² = a² + 2ab + b² pode ser usada para calcular eficientemente a área de figuras geométricas compostas. Por exemplo, imagine um terreno retangular com dimensões (x + 3) metros e (x + 2) metros. Para calcular a área total, poderíamos expandir a expressão (x + 3)(x + 2) utilizando a propriedade distributiva, ou, se reconhecermos que podemos aproximar as dimensões a um quadrado com lado (x+2,5) aproximadamente, poderíamos usar o quadrado da soma para estimar a área, obtendo um valor aproximado de (x+2,5)² = x² + 5x + 6,25 m².
Este método, embora aproximado, oferece uma solução rápida e eficiente em situações onde a precisão absoluta não é essencial.
Diagrama Ilustrativo da Aplicação Geométrica
Imagine um quadrado grande dividido em quatro partes. A parte superior esquerda é um quadrado menor com lado “a”, representando a área a². A parte inferior direita é outro quadrado menor com lado “b”, representando a área b². As duas partes restantes são retângulos, cada um com lados “a” e “b”, representando a área ab. Juntando as áreas, temos a² + ab + ab + b² = a² + 2ab + b², que é a área total do quadrado grande com lado (a + b).
Essa representação visual demonstra concretamente a identidade (a + b)² = a² + 2ab + b². A área total do quadrado grande, (a+b)², é a soma das áreas dos quatro menores componentes, demonstrando geometricamente a validade da fórmula.
Dominar o quadrado da soma é essencial para o sucesso em matemática, abrindo portas para a resolução de problemas mais complexos. Após explorarmos 10 exemplos distintos e suas soluções detalhadas, você estará apto a aplicar essa fórmula com confiança e precisão em diferentes contextos. Lembre-se: a prática leva à perfeição! Continue explorando e resolvendo exercícios para consolidar seu aprendizado.
Boa sorte e bons estudos!

